在人类文明的数学殿堂中,有一个看似抽象的问题却可能在瞬间颠覆我们的数字世界:黎曼猜想。这个已经困扰数学家160多年的千禧年大奖难题,不仅被牛津大学数学教授马库斯·杜·索托伊称为”危险的”,更与我们每天使用的网络支付、在线购物和数字通信的安全息息相关。当数学理论与现实世界发生碰撞时,一个看似纯粹的学术问题为何会成为现代文明的潜在威胁?
从抽象符号到现实威胁的惊人转变
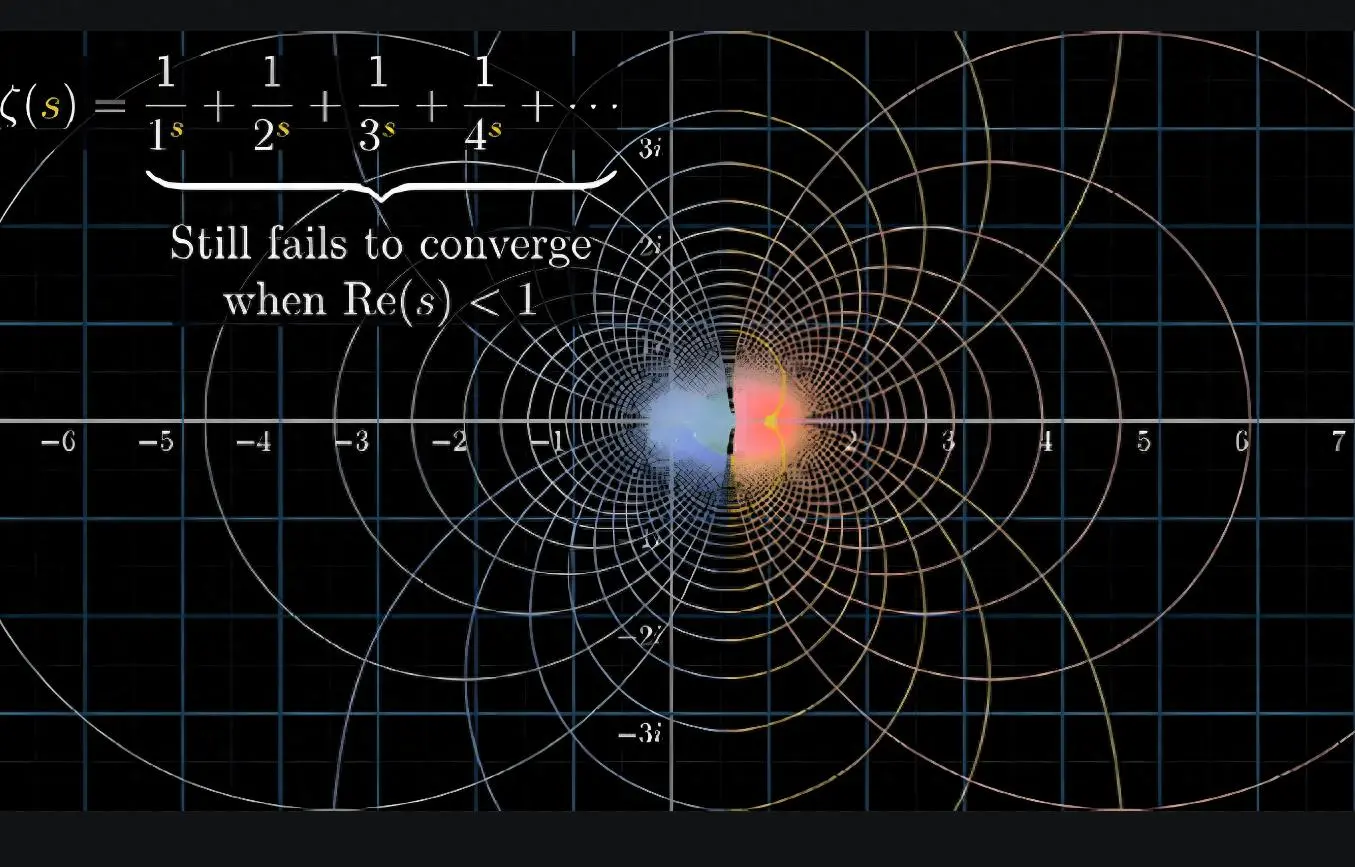
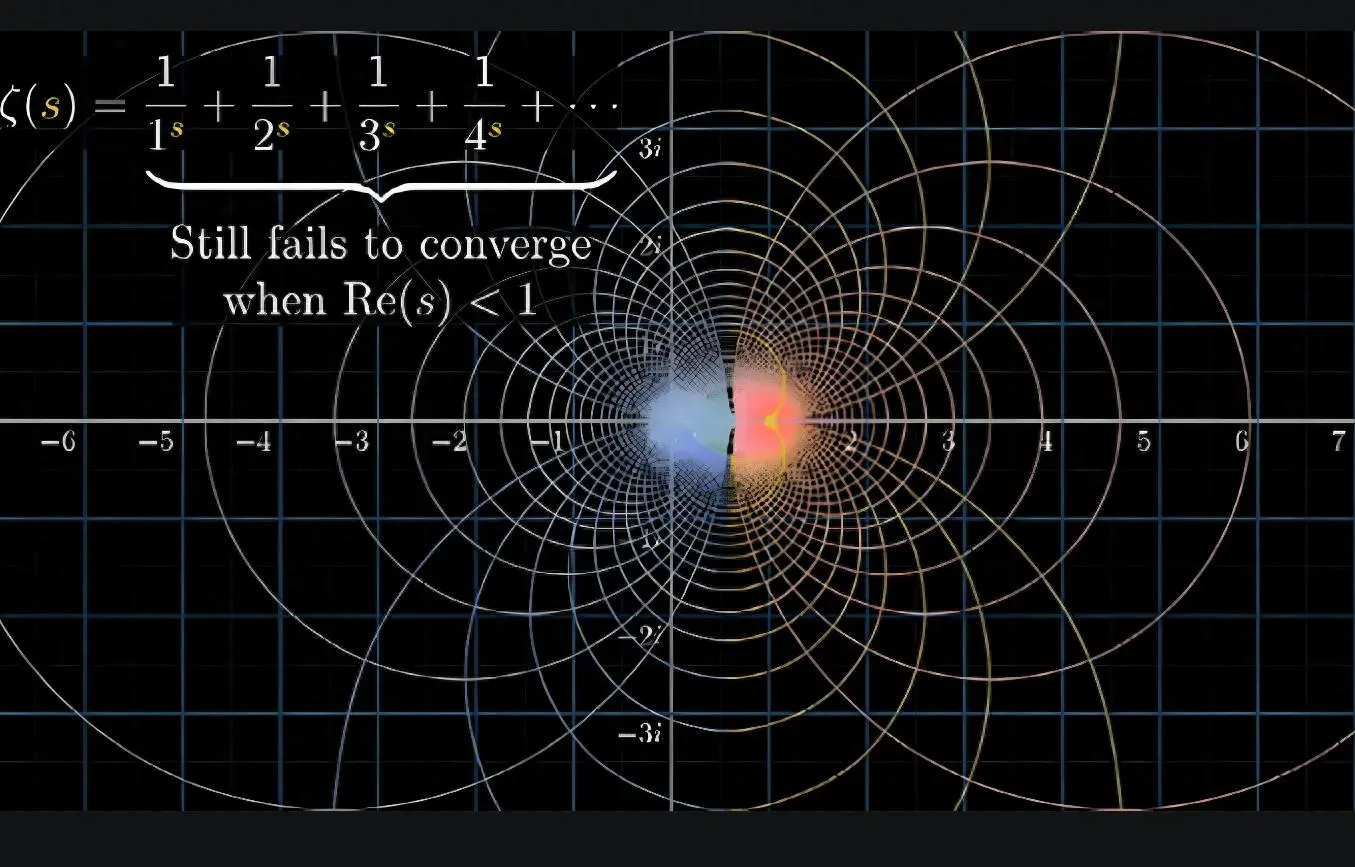
黎曼猜想表面上只是一个关于数学函数零点分布的技术性问题,它断言黎曼ζ函数的所有非平凡零点的实部都等于1/2。对于普通人而言,这个表述如同天书一般晦涩难懂。然而,索托伊在其著作《悠扬的素数:黎曼猜想趣史》中揭示了一个令人震惊的事实:这个抽象的数学命题一旦被证实或证伪,都将对现代社会产生颠覆性的影响。

黎曼猜想的”危险性”首先体现在其对数学理论体系的巨大冲击力上。目前有数以百计的重要数学定理是建立在”假设黎曼猜想成立”这一前提之上的。如果这个猜想最终被证实,这些定理将立即升级为绝对真理,极大地完善数论的理论基础;但如果被证伪,整个数论领域将面临一场史无前例的重构,无数研究成果可能需要重新审视甚至推翻。
更为关键的是,黎曼猜想直接关联着素数分布规律的深层奥秘。素数作为数学中的”原子”,其分布模式一直是数学家试图破解的核心谜题。如果黎曼猜想被证实,人类对素数分布的理解将达到前所未有的精确度;如果被证伪,则意味着素数的分布可能比我们想象的更加混乱和不可预测,这将迫使数学家寻找全新的理论框架。
然而,真正让黎曼猜想变得”危险”的,是它与现代密码学的紧密联系。目前广泛应用于网络安全的RSA加密系统,其安全性完全建立在大数分解的困难性之上——具体来说,就是将一个巨大的数分解为素数因子的计算复杂性。正是这种计算的”困难性”,保护着我们每天进行的网络交易、电子邮件通信和在线身份验证。
从逾越节酒宴到互联网安全基石的传奇诞生
RSA加密系统的诞生本身就是一个充满戏剧性的故事。1977年,麻省理工学院的三位研究者——罗纳德·李维斯特、阿迪·沙米尔和伦纳德·阿德曼在一次逾越节聚餐后,灵感迸发,创造出了这个至今仍在保护全球互联网安全的加密算法。
这个系统的巧妙之处在于其非对称性设计:它使用两把不同的”钥匙”,一把用于加密信息,另一把用于解密。这种设计彻底解决了传统密码学面临的密钥分发难题,使得陌生人之间的安全通信成为可能。更重要的是,RSA的安全性完全依赖于一个看似简单的数学事实:将两个大素数相乘很容易,但将它们的乘积重新分解回原来的素数却极其困难。
1903年,纽约哥伦比亚大学的数学教授弗兰克·纳尔逊·科尔用三年时间,牺牲所有周日下午,才成功分解了一个仅有20位数的梅森数。这一壮举在当时被视为数学奇迹,引来全场起立鼓掌。然而,现代RSA加密使用的数字通常有数百位甚至上千位,其分解难度呈指数级增长。正是这种计算复杂性的保护,我们的银行卡号、密码和个人信息才能在互联网上安全传输。
然而,这个看似坚不可摧的安全堡垒,却可能因为黎曼猜想的解决而瞬间坍塌。如果数学家能够深入理解素数的分布规律,就有可能开发出更高效的因数分解算法,从而彻底破解RSA加密系统。这意味着,一个纯数学理论问题的突破,可能在一夜之间让全球的网络安全体系变得形同虚设。
数学理论突破与现实安全风险的深层博弈
黎曼猜想解决所带来的潜在冲击远不止于密码学领域。解决这一问题所需要的全新数学工具和方法,很可能引发整个数学学科的革命性变革。正如费马大定理的证明催生了椭圆曲线和模形式理论的巨大发展一样,黎曼猜想的解决可能会开辟全新的数学研究领域,推动几何、分析、拓扑、代数、概率论等多个分支的深刻发展。
这种数学理论的进步虽然令人振奋,但也带来了现实的安全担忧。当前的互联网基础设施、电子商务系统、数字货币网络以及国家安全通信系统,都建立在现有密码学技术的基础之上。如果这些技术因为数学理论的突破而变得脆弱,整个数字文明的安全根基都将面临威胁。
更复杂的是,黎曼猜想的证明或证伪都可能带来意想不到的后果。即使证明了这个猜想,新的数学工具也可能被用于开发更强大的攻击算法;而如果猜想被证伪,素数分布的不规律性可能会导致现有加密系统出现意想不到的漏洞。
面对这种不确定性,密码学研究者已经开始着手开发”后量子密码学”技术,试图构建即使在量子计算和高级数学理论双重威胁下仍然安全的加密系统。这些新技术不再依赖于因数分解问题的困难性,而是基于其他数学难题,如格理论或椭圆曲线上的问题。
有趣的是,这种”数学武器竞赛”实际上推动了整个科学技术的进步。正如索托伊所指出的,数学理论的每一次重大突破,都会带来技术应用的连锁反应。黎曼猜想的最终解决,无论结果如何,都将为人类知识的边界拓展做出重要贡献。
在这场数学与现实的博弈中,我们既要为人类智慧的进步感到兴奋,也要为潜在的安全挑战保持警惕。黎曼猜想之所以被称为”危险的”,正是因为它完美地体现了纯数学理论与现实世界之间错综复杂的联系。在数字化时代,没有任何数学发现是纯粹抽象的——每一个理论突破都可能在瞬间改变我们的生活方式。